3.2. Бинарный (двоичный) поиск
Если линейный поиск медленный, но умеет работать с любыми массивами, существует и поиск, который работает быстрее, но только на определённых данных — бинарный поиск. Это поиск, который может вызываться только на отсортированных массивах данных (о том, почему массив должен быть именно отсортированным, узнаем чуть позже). Бинарный поиск обычно работает по типу indexOf. Он принимает элемент, который нужно найти в массиве, и возвращает либо его позицию, либо -1, либо null.
Думаем, многие пользовались бинарным поиском ещё с детства, например, при чтении энциклопедий. Предположим, вам было интересно узнать, что же такое «Калган». Искать это слово линейным поиском в отсортированной в алфавитном порядке энциклопедии — довольно долго. Нужно пролистать около четверти книги, чтобы его найти. Гораздо легче открыть книгу примерно посередине и посмотреть, в какое слово мы попали. «Растение»? «Р» гораздо дальше по алфавиту, чем «К». Можно разделить нашу книгу пополам от начала и до места, где мы сейчас находимся, и посмотреть на первое слово оттуда. «Ива»? «И» чуть раньше по алфавиту, чем «К». Разобьём часть от «И» до «Р» пополам и посмотрим на элемент посередине... И так далее, пока не найдём нужное нам слово.
Такой быстрый поиск мы смогли совершить благодаря упорядоченности данных. Ведь если бы автор энциклопедии решил не размещать слова в алфавитном порядке, а просто писал их по мере вспоминания, то открытие книги посередине вполне могло бы нам дать слово «Автор», а наш «Калган» мог находиться на первой странице. Тогда и отсеивать сразу по половине слов, которые нас не интересует, мы не смогли бы. Так как нет никаких гарантий, что в отброшенной по принципу «левее — меньше, правее — больше» половине не могло оказаться нашего слова.
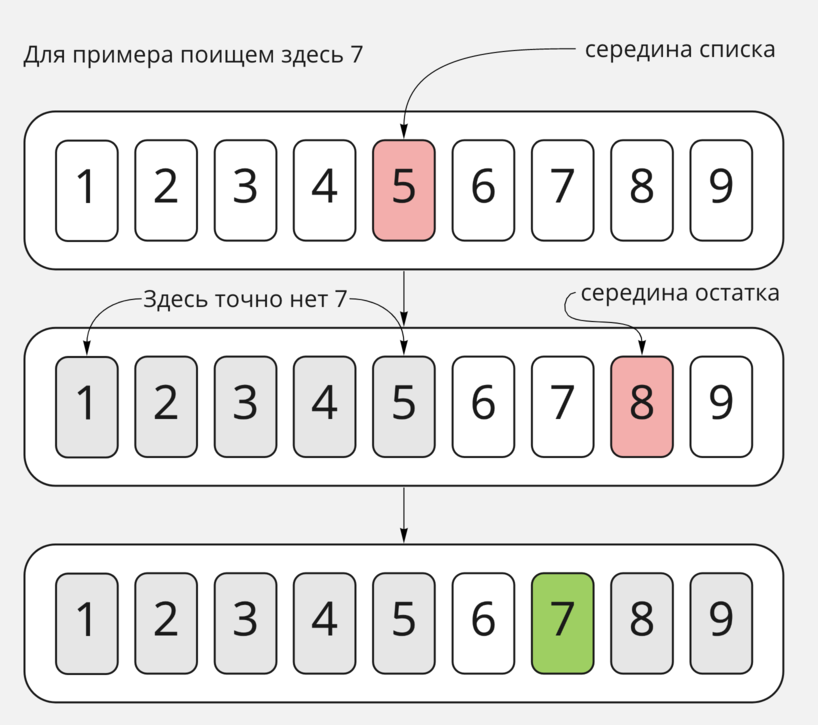
Пример бинарного поиска
Если говорить о применении таких «поисков по энциклопедии» в программировании, то бинарный поиск используют «под капотом» базы данных. Когда вы пробуете войти на каком-нибудь сервисе в свой аккаунт с логином «giantmonster1991», ему нужно будет сначала проверить, существует ли такой пользователь вообще. Если искать пользователя линейным поиском в базе на миллионы человек, на это может уйти уйма времени! А вот сужение поиска отбрасыванием сразу половины элементов существенно ускоряет его. Давайте посмотрим, насколько бинарный поиск быстрее обычного: имея базу в миллион пользователей, мы будем в худшем случае проверять логин на наличие миллион итераций, а в бинарном поиске, сокращая каждый раз количество просматриваемых элементов в два раза, нам потребуется всего 20 итераций в худшем случае! (1000000 -> 500000 -> 250000 -> 125000 ->... -> 15 -> 7 -> 3 -> 1).
Очевидно, что бинарный поиск работает очень быстро, гораздо быстрее линейного. Но насколько? Как оценить скорость такого алгоритма?
Логарифмы
Всё-таки придётся вспомнить логарифмы, которые мы так пытались обойти стороной при введении сложности сортировок... На самом деле, в логарифмах, даже если вы их совсем забыли, нет ничего страшного. Это просто операция, обратная возведению в степень: если 2⁴ — это 16, то log₂16 — 4. То есть когда мы пишем log₂16, мы спрашиваем «Сколько раз надо перемножить двойку саму на себя, чтобы получить 16?». Ответ на этот вопрос как раз 4.
Здесь и далее, когда мы будем разговаривать о логарифмах в разрезе алгоритмической сложности, мы будем подразумевать именно логарифм по основанию два или log₂n.
Причём здесь бинарный поиск? Если вернуться к нашему примеру с миллионом пользователей в базе, то log₂1000000 даёт нам чуть меньше, чем 20. Если попробуем поискать среди 16 элементов, то получим (16 -> 8 -> 4 -> 2 -> 1) 4 итерации сужения поиска, а log₂16 как раз и есть 4. Не будем доказывать формально, но, как видно на примерах, бинарный поиск занимает логарифм по основанию два от количества элементов итераций. Перекладывая в уже знакомую нам O-нотацию, мы можем записать это как O(log(n)). Заметьте, что основание мы не написали — мы можем его опускать, потому что при оценке алгоритмов почти всегда используем именно логарифм по основанию два. Немного намекнём на будущее, и в оценке сортировки (O(n*log(n))) логарифм стоит не просто так, там происходят подобные операции.
Если математическое описание сложности не показывает, насколько ускоряется этот алгоритм по мере увеличения количества данных, взгляните на эту таблицу:
| Количество элементов | 1 | 16 | 1000 | 1000000 | 1000000000 |
|---|---|---|---|---|---|
| Итерации линейного поиска | 1 | 16 | 1000 | 1000000 | 1000000000 |
| Итерации бинарного поиска | 1 | 4 | 10 | 20 | 30 |
Впечатляет, правда? Давайте попробуем написать свой бинарный поиск и убедимся в его эффективности на практике в следующем демо.