Помимо DOM, существует огромное количество специализированных деревьев, которые позволяют решать стандартные задачи. Давайте познакомимся с ещё одним видом деревьев — бинарным деревом поиска (Binary search tree, BST). Эта статья ознакомительная: она не даст глубокого понимания BST, потому что для раскрытия всех аспектов (даже простого добавления элемента) потребуется много теории, а на практике во фронтенде его встретить практически невозможно. Тем не менее это одно из самых популярных видов деревьев, а ещё о нём довольно часто поверхностно спрашивают на собеседованиях в крупные компании. Так что хотя бы знать о его существовании — хорошее подспорье!

«Бинарное» (двоичное) оно, потому что у каждой ноды может быть не более двух «детей». А «поиска» — из-за того, что оно упорядочено таким образом, что позволяет быстро находить в нём нужную информацию. То есть упорядочено оно таким образом, что если мы посмотрим на любую ноду, то левый её ребенок и все его дети рекурсивно будут меньше неё, а все дети справа — больше или равны. Посмотрим на простенький пример такого дерева:

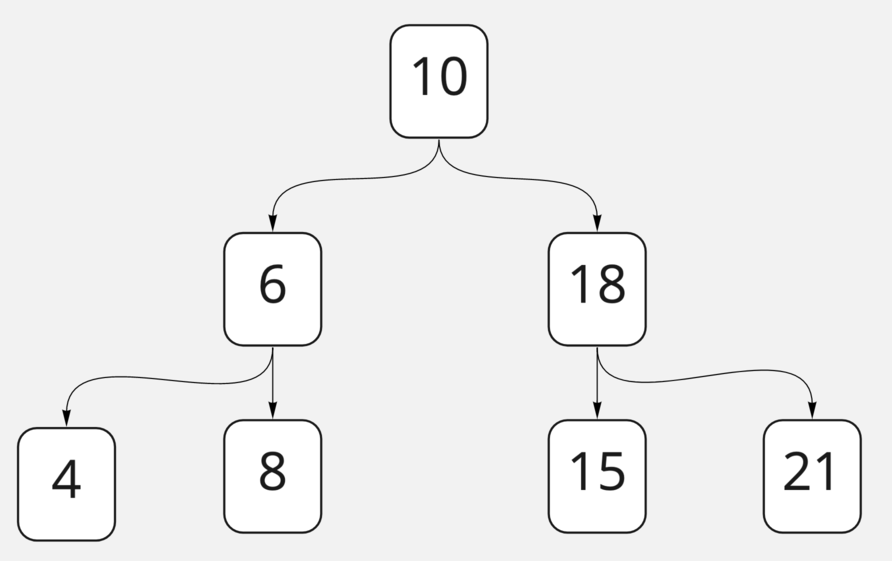
Сбалансированное бинарное дерево поиска

Поиск по такому дереву будет напоминать подобие бинарного поиска — они даже называются похоже! Мы начинаем с «середины» дерева, и если искомый элемент будет больше или равен середине, то «спускаемся» в правую часть дерева, а если меньше — в левую. В нашем примере худший случай поиска — поиск чего-либо с самого нижнего уровня дерева, например 8. Поиск займёт у нас три операции: надо будет пройти 10, 6 и 8. Всего элементов у нас семь, поэтому количество операций при поиске в худшем случае примерно равно logn. Это даёт нам сложность O (logn), как и у бинарного поиска! Однако в отличие от поддержания сортированности обычного массива, которое занимает у нас O (n) для сортировки вставкой, операция вставки в бинарное дерево уже подразумевает, что дерево останется упорядоченным, и вставка занимает всего O (logn).

Вы можете апеллировать тем, что можно модифицировать сортировку вставкой так, чтобы она искала место вставки бинарным поиском за O (logn). Но не забывайте, что помимо поиска места вставки, нам нужно также вставить элемент, а это займёт O (n). Помните, что «под капотом» нам нужно подвигать каждый элемент после вставляемого на один вправо?

Однако всё так радужно, пока наше дерево является сбалансированным, то есть количество нод в левом и правом поддереве примерно равны. Если бы мы построили дерево из примера выше другим образом, например вот так:

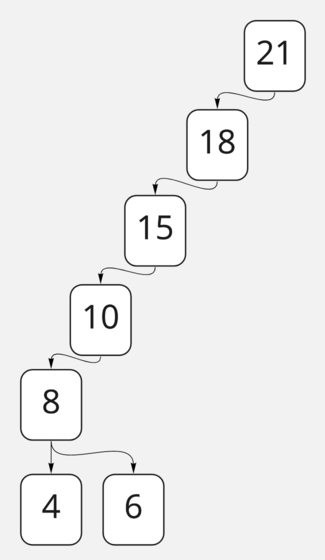
несбалансированное бинарное дерево поиска

...то сложность поиска четвёрки была бы близка к сложности обычного линейного поиска. Поэтому важно держать наше дерево хотя бы примерно сбалансированным. Для этого существуют так называемые самобалансируемые деревья поиска, в которых балансировка происходит при каждой вставке, а сложность её всё равно остаётся O (logn). Это довольно сложный концепт, который вы вряд ли будете применять на практике, а во всех «библиотечных» деревьях поиска он уже реализован за вас. Однако если вы хотите знать больше, то можете прочитать об алгоритмах самобалансировки в этой неплохой статье.

Деревья поиска применяются как раз для поддержания сортированности данных и быстрого доступа к ним впоследствии. Самое частое применение этих деревьев — построение индексов для баз данных. Когда мы запрашиваем данные с API, отсортированные по возрастанию по какому-либо из полей, база данных как раз использует построенные «под капотом» представления бинарных деревьев поиска, чтобы быстрее обработать ваш запрос. И именно поэтому чем больше индексов построено в базе, тем дольше отрабатывает вставка: все-таки надо сбалансировать «подкапотные» деревья. Так что, если у вас подтормаживают какие-то запросы, можете прийти к вашей команде бэкенд-разработки и уточнить, есть ли нужные вам индексы.

Посмотрим на решение задачи с поиском трёх максимальных счетов из прошлого раздела при помощи такого дерева.