Сортировка пузырьком — это один из самых простых для понимания и реализации методов сортировок. Однако из-за отсутствия каких-либо оптимизаций работает он очень медленно (насколько — не скажем, оценим чуть позже), поэтому и на практике практически не применяется. Этот алгоритм является устойчивым и использует операции сравнения — огромное количество!

Суть алгоритма

Мы проходимся по всему массиву и по мере прохода сравниваем каждые соседние числа между собой. Если порядок в этой паре неправильный — меняем их местами, а если всё верно — просто двигаемся дальше. Тогда после первого прохода наибольший элемент точно окажется в самом конце массива — ведь мы сравнили его с каждым предыдущим, и он оказался больше каждого другого элемента. После окончания первой итерации мы можем исключить последний элемент из процесса сортировки, он уже на своём месте, и начнём сортировать массив из всех элементов, кроме последнего. Таким образом, совершаем количество элементов в списке - 1 итерацию для сортировки всего массива или завершаем процесс, когда на очередной итерации мы не выполнили ни одной перестановки.

Именно такое поведение, из-за которого наибольший элемент после очередной итерации оказывается в конце массива, и дало ему это название: наибольшие элементы, как пузырьки, как бы «всплывают» в конец массива.

Пример сортировки

Перед тем, как приступить к оценке и написанию нашей первой сортировки, посмотрим на простой пример её работы на небольшом массиве из целых чисел: [4, 3, 5, 2, 1].

Начнём первую итерацию. Посмотрим на два первых элемента: 4 и 3. Так как 4 больше, чем 3, поменяем их местами.

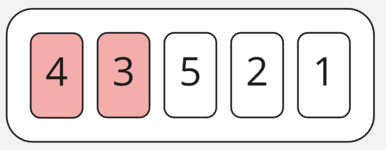
Затем смотрим на 4 и 5. Здесь всё хорошо, 4 меньше, чем 5, поэтому оставляем их на своих местах и двигаемся дальше.

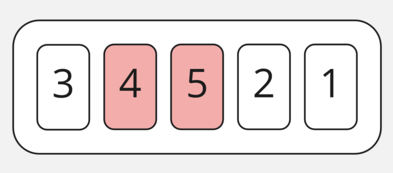
Приходим к сравнению 5 и 2. 5 больше, чем 2, поэтому меняем их.

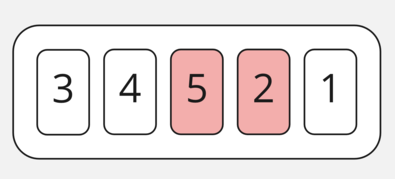
И в последнем шаге меняем 5 и 1.

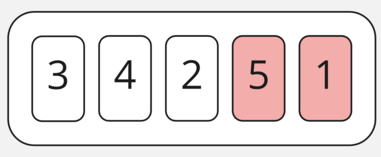
В итоге мы получили справа отсортированную часть массива, состоящую всего лишь из одного элемента, который мы успели туда «довести», а слева — часть, на которой мы продолжим выполнять сортировку таким же образом.

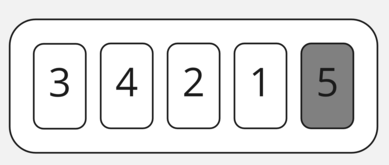
В начале второй итерации мы снова сравниваем 3 и 4 — вот и первые отголоски неоптимизированности: повторение одинаковой работы с одними и теми же данными. Мы их уже трогали на предыдущей итерации, поэтому больше ничего не делаем.

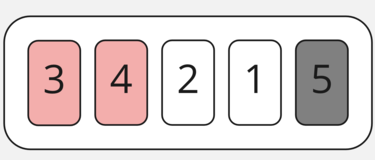
Затем сравниваем 4 и 2. Так как 4 > 2, меняем их местами.

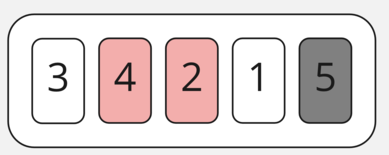
И то же самое делаем с 4 и 1.

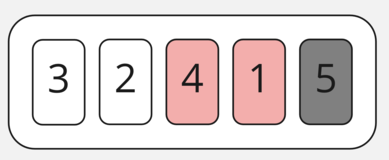
В итоге получаем прирост к нашей отсортированной части массива, которую мы не будем трогать, ура-ура!

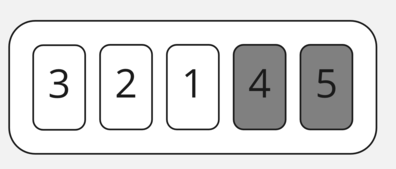
В третьей итерации нам нужно пройтись по трём элементам и помочь «всплыть» тройке.

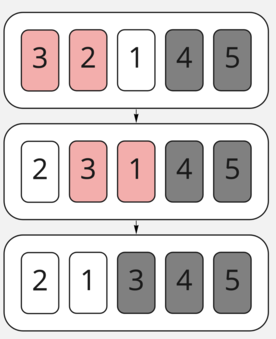
А в последней — всего лишь поменять оставшиеся два элемента местами.

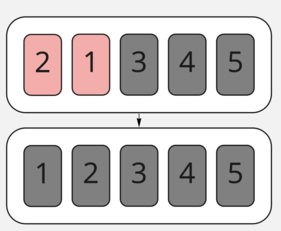
Последняя итерация прибавила сразу два элемента в нашу отсортированную часть массива и завершила сортировку.

Оценка по времени и по памяти

Прежде чем читать дальше, попробуйте оценить этот алгоритм сами!

Так как мы совершили (n - 1) итерацию, в каждой из которых мы последовательно сравнивали (n - номер итерации + 1) пар чисел, общая сложность этой сортировки в худшем случае будет O((n-1)(n-<некая константа>)), а при упрощении — O(n²). По памяти этот алгоритм занимает O(1), если не считать входной массив — изменяем мы его «на месте», дополнительную память нам использовать незачем.

Хотя мы и говорили, что правильно оценивать только худший из всех возможных вариантов входных данных при выполнении алгоритма, для сортировок ситуация немного иная. Иногда разработчики знают, какие примерно данные придут на вход, поэтому могут использовать алгоритмы, которые не очень хорошо работают в худших случаях, но лучше подходят в случае с «почти отсортированными» данными. Так вот, в лучшем случае, если массив уже отсортирован, алгоритм сортировки пузырьком отработает всего за O(n)! Для этого нужно немного его модифицировать: если мы ничего не поменяем в рамках первой итерации, то таким образом просто проверим сортированность массива и скажем, что всё хорошо. Ну, а если вдруг у нас будет чуть худшая ситуация с парой-тройкой выбивающихся элементов, проходов будет столько же соответственно.

Это подводит к ещё одному достаточно важному правилу использования алгоритмов: не злоупотребляйте алгоритмами, которые дают лучший результат в самом общем случае! Лучше проанализируйте, подходит ли конкретно для ваших случаев что-то лучшее, чем «средне-лучший» алгоритм.

А теперь давайте попробуем реализовать эту сортировку самостоятельно!