Потому что это одна из самых быстрых сортировок для использования на больших объёмах неотсортированных данных. Она сложнее для понимания и реализации. Но если не заходить в дебри её оптимизации, она довольна проста, чтобы с ней познакомиться.

Суть алгоритма

• Выбираем в массиве «опорный» элемент. Им может быть абсолютно любой элемент из массива, однако чуть дальше мы поговорим о том, как его выбор влияет на время выполнения.
• Сравниваем каждый из элементов массива с опорным элементом и по результату сравнений переставляем элементы в нашем массиве так, чтобы слева от опорного были все элементы меньше него, а справа — больше или равны.
• Запускаем этот же алгоритм рекурсивно на левую и правую части массива, пока не придём к массиву из одного элемента.

Можно заметить, что этот алгоритм разделяет наши данные на части и «властвует» над каждой из них! Вот и ещё один алгоритм в копилку Divide-and-Conquer. А из-за того, что элементы могут перемешаться в процессе «перекидывания» вокруг опорного элемента, эта сортировка не является устойчивой.

Пример сортировки

Посмотрим на сортировку массива из девяти элементов quicksort-ом. Для начала выберем опорный элемент и переместим элементы меньше слева от него, а элементы больше — справа.

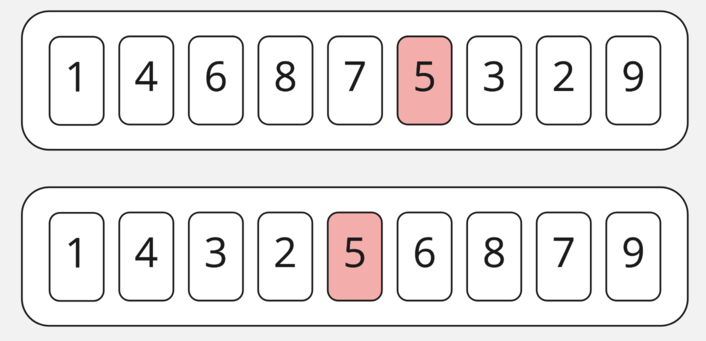
Затем возьмём часть слева от опоры и сделаем там то же самое.

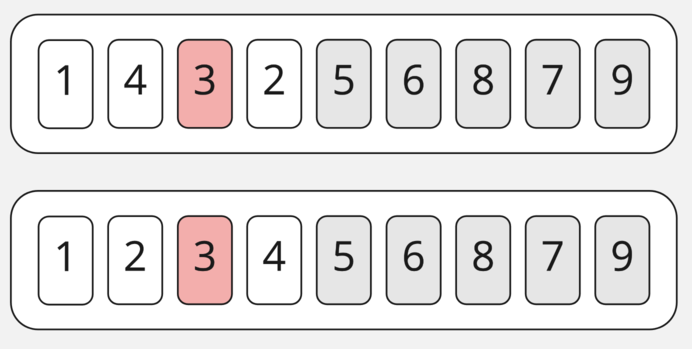
Когда мы выберем опору, то поймём, что в целом у нас получились массивы из одного элемента. При необходимости переставив их местами (у нас такой необходимости нет), пометим эту часть массива отсортированной и перейдём к сортировке следующего «подмассива».

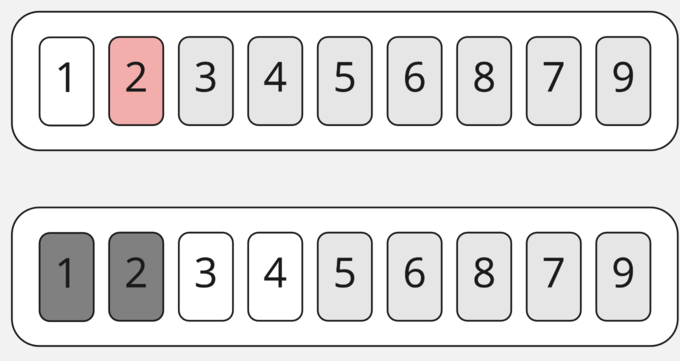
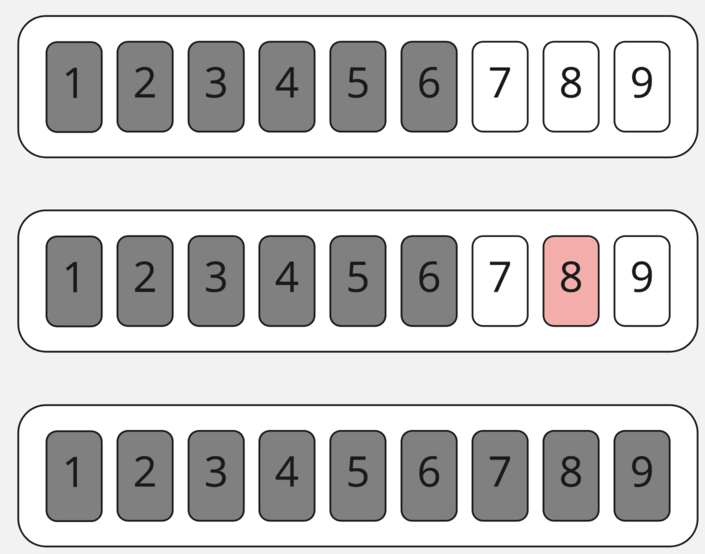
Здесь получаем то же самое, что и на прошлом шаге — подмассивы длинной в 1. Опустим их сортировку и пойдём сортировать правую часть массива.

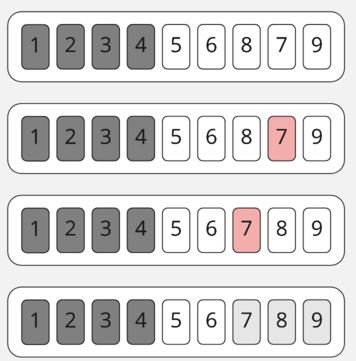
Получаем в итоге два массива из двух и трёх элементов, которые мы уже умеем сортировать.

В итоге мы при помощи сведения задачи к более простым, сортировке массивов из одного–двух элементов, быстро отсортировали массив!

Оценка по времени и по памяти

Прежде чем читать дальше — попробуйте самостоятельно оценить получившийся у нас вариант!

Как и в любом Divide and Conquer алгоритме у нас получилось свести эту задачу к logn подзадач, а сами операции разделения (переноса элементов влево и вправо) занимают n операций. Итого в нашем случае имеем сложность O(n*logn). При этом мы совсем не выделяли дополнительную память — получили O(1) по памяти.

Но это далеко не худший случай! Если бы мы имели уже отсортированный массив и выбирали опорным самый первый из его элементов, то сделали бы O(n²) операций, потому что у нас в итоге появилось бы n подзадач: мы «срезали» бы нашу задачу не вполовину, а всего на один элемент. Поэтому выбор опорного элемента играет важную роль в работе quicksort.

Выбор опорного элемента

Чтобы уверенно делить задачу на подзадачи, работающие с половиной исходных данных, нам нужно научиться всегда попадать в медиану списка (элемент, который в отсортированном массиве будет лежать ровно посередине) или хотя бы близко к ней.

Частый способ «побороть» эту проблему — просто выбирать случайный элемент или элемент из текущей середины. Так мы достаточно минимизируем риски попасть в наименьший или наибольший элемент массива в «почти отсортированных» данных. Есть способ найти и настоящую медиану за линейное время, не повлияв таким образом на сложность в O(nlogn). Но это довольно сложная операция. Почитать о том, как это делается, можно здесь.

В следующем демо попробуем самостоятельно написать быструю сортировку.