Чтобы перейти к сортировке вставкой, стоит ввести ещё одну структуру данных, иногда применяемую на практике: связный список. В вебе она встречается очень редко — ситуации, в которых он даёт преимущество по производительности хотя и есть, но зачастую не стоят того.

Что это?

Связный список — это структура данных из элементов, состоящих из узлов (нод), которые содержат в себе какие-то данные и один-два указателя на другой узел или null, если связи с другими узлами нет. Чтобы было понятнее, давайте посмотрим на примере.

Двусвязный список

На самом деле, «под капотом» уже известное всем фронтенд-разработчикам DOM-дерево хранит узлы дерева на одном уровне вложенности как двусвязный список! Речь сейчас идёт о свойствах nextSibling и previousSibling.

Посмотрим на следующий код:

<section>
  <p>Первый параграф</p>
  <p>Второй параграф</p>
  <p>Третий параграф</p>
</section>

p внутри section организованы примерно так:

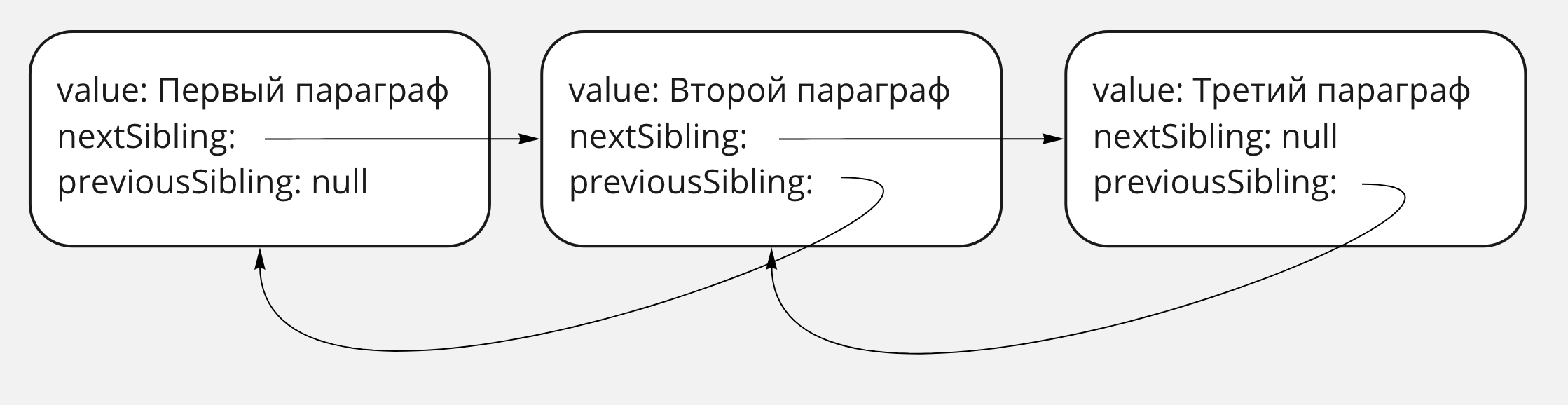
Но для более простого представления связные списки обычно схематически показываются вот так:

Таким образом, мы не можем изнутри каждого параграфа обратиться к любому из его соседей по индексу, но умеем получать его следующего или предыдущего соседа. Это и есть двусвязный список

Односвязный список

Как следует из названия, это примерно то же самое, что и пример сверху, только с одной связью. Как если бы мы в примере сверху имели доступ только к следующему соседу, а предыдущего узнать уже не могли. Пример использования такого списка мы увидим в следующей статье.

Алгоритмические сложности операций над списками

Когда мы говорим, что мы работаем со связным списком, то подразумеваем, что у нас имеется его «голова» — первый элемент. И уже от него мы можем получить остальные элементы, передвигаясь по указателям на следующие элементы. Тогда обход и поиск будут работать всё также за O(n), а «случайного» доступа по индексу у нас нет, ведь нет и самого по себе индекса. Однако если мы захотим получить n-й элемент списка, то вместо O(1) у массива (простое обращение array[n]), мы получим O(n) — нам надо пройти n-1 ссылку, чтобы получить нужный элемент.

Однако удаление и вставка в начало отрабатывает за O(1) — нам нужно либо (при удалении) просто достать следующий элемент от «головы» и положить его как новую голову, либо (при вставке) указать во вставляемой ноде следующим элементом нашу текущую «голову» и положить вставляемый элемент в переменную с началом списка. Если имеем указатель и на конец, то за такую же сложность можем делать те же операции и с ним.