Это одна из немногих сортировок, которая работает в «онлайн режиме» — помогает поддерживать отсортированность в уже существующем массиве при поступлении новых элементов.

Суть алгоритма

При получении очередного элемента для вставки в массив мы начинаем продвигаться по этому массиву слева направо. Сравниваем вставляемый элемент с текущим. Если он меньше текущего, то идём сравнивать его со следующим, а если больше — вставляем его на эту позицию и сдвигаем каждый из элементов на один вправо (в случае со связным списком указываем вставляемой ноде родителем предыдущий элемент, а ребёнком — тот, на котором остановились).

Пример сортировки

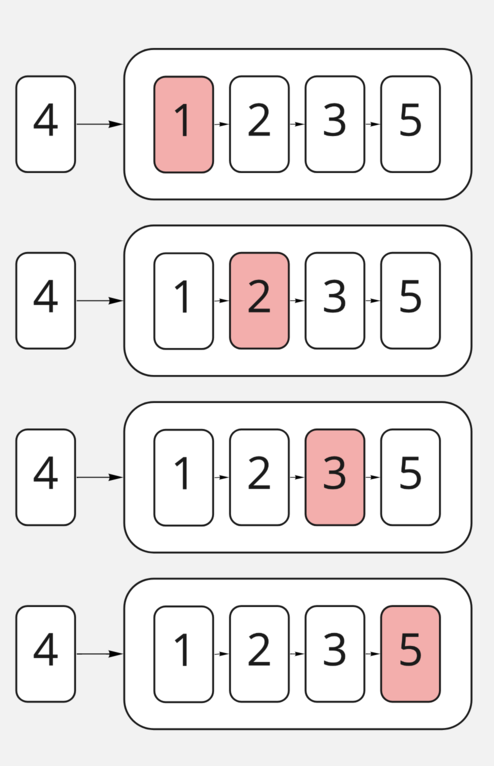
Посмотрим на самый простой случай вставки в маленький связный список из чисел.

Сначала будем проходить по нему до тех пор, пока не встретим элемент, который больше вставляемого.

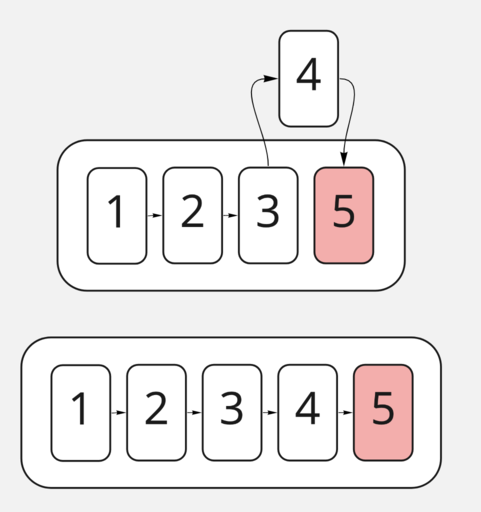
А затем обновляем связи в нашем списке.

Оценка по времени и памяти

Прежде чем читать дальше, попробуйте оценить сложности самостоятельно!

В худшем случае нам пришлось бы пройти список целиком, прежде чем вставить туда нужный элемент, что занимает O(n), а сама вставка занимает O(1) — переопределение «родства» в списке не зависит от входных данных. Дополнительную память мы использовали только для того, чтобы следить за позицией текущей итерации в списке, так что получаем O(n). При работе с массивом сложность бы не поменялась, разве что вместо простого обновления связей нам придётся двигать всю часть после вставленного элемента на одну позицию вправо. Как мы знаем из введения в стеки и очереди, это занимает O(n).

В следующем задании применим полученные знания на практике!