Перед тем, как мы перейдём к разговору о деревьях, давайте узнаем о структуре, на которой они строятся — графе.

Граф — это структура данных, которая позволяет нам связывать данные между собой. Например, графами можно смоделировать связи людей в социальных сетях. Так если у нас есть два пользователя, Саша и Таня, и они находятся в друзьях друг у друга, то можно визуализировать их связь вот таким графом:

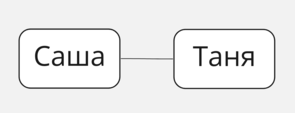
Простой граф друзей

Здесь есть два объекта и одна связь. Собственно, это и есть единственные составляющие графа.

Такие объекты ещё называют «нодами» (англ. node), «вершинами» или реже — «узлами». А связь зазывают «ребром» (англ. edge).

Свойства графов

Ориентированность

Если мы уйдем от социальных сетей, в которых можно быть друзьями только по обоюдному согласию, в сторону тех, в которых используется система подписок, то наш простенький граф из примера выше перестанет работать. Глядя на него, мы не сможем понять: только Саша подписана на Таню, Таня на Сашу или у них взаимная подписка. Чтобы он снова стал репрезентативным, введём направление у связей:

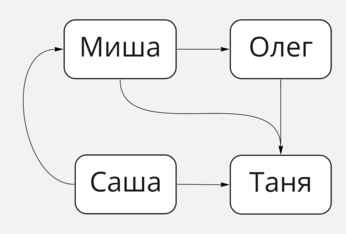
Чуть более сложный граф подписчиков

Такой граф называется ориентированным или направленным.

Цикличность

Тут всё просто: если мы можем из одной точки графа попасть в неё же через несколько перемещений, то этот граф называется циклическим графом. В примере выше мы не сможем найти цикл, из какой бы вершины мы ни начали путь. Дорисуем одну связь, чтобы появился цикл:

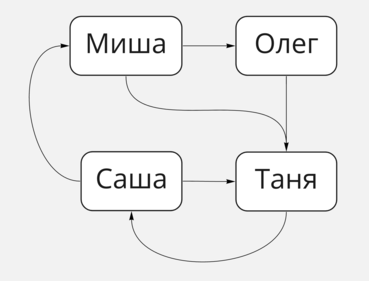
Циклический граф

В этом графе у нас есть цикл длиной 4: Миша-Олег-Таня-Саша.

Циклы также могут быть длиной 0, если есть ребро, которым нода связана сама с собой. Обычно такие циклы называют петлями.

Связность и полнота

Граф связный, если из любой вершины есть путь в любую другую вершину, и полный, если между каждыми нодами есть путь, состоящий из всего одного ребра.

Взвешенность

Каждому ребру графа можно тоже можно присвоить какую-то информацию. Например, если у нас имеется граф с точками на карте и нам нужно сохранить информацию о расстоянии между ними, то мы можем написать её рядом с каждым ребром. Графы, у которых рёбра имеют подобным образом хранимую информацию, называют взвешенными.

Представление в коде

Часто можно встретить графы, представляющие собой объект, в котором описаны все вершины одним списком и рёбра в формате массива пар вида [нодаНачала, нодаКонца]. Например, этот граф:

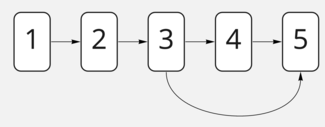
Можно представить в коде примерно таким образом:

const graph = {
  nodes: [1, 2, 3, 4, 5],
  edges: [
    [1, 2],
    [2, 3],
    [3, 4],
    [3, 5],
    [4, 5],
  ]
};

С этим довольно просто работать: добавление, поиск и удаление из него сведётся к уже привычным операциям над массивами.

Однако так уж повелось, что в вебе чаще всего при работе с графами (поиске по ним, обновлении, поиске циклов) мы работаем с сущностями по типу нод уже знакомых нам связных списков:

const node = {
  value: 'some info',
  neighbours: [otherNode, anotherNode],
}