Шаг 1

Итак, возвращаемся к нашей предыдущей задаче — поиску топовых игроков. Так как построение деревьев поиска с нуля является довольно сложной алгоритмической задачкой, построим небольшое дерево «руками». Просто продемонстрируем технологам, что единоразовый перевод данных в более подходящий формат делает задачу куда проще и предотвращает дальнейшие проблемы.

import {log} from "./logger";

const data = [
  {
    "login": "DreamLess",
    "leaguePoints": 956
  },
  {
    "login": "cavernous",
    "leaguePoints": 1056
  },
  {
    "login": "SaiyanBroadway",
    "leaguePoints": 1432
  },
  {
    "login": "Mountaintrid",
    "leaguePoints": 1130
  },
  {
    "login": "cathead",
    "leaguePoints": 930
  },
  {
    "login": "Goldenelox",
    "leaguePoints": 932
  },
  {
    "login": "BoostScooby",
    "leaguePoints": 1476
  },
  {
    "login": "JoshChase",
    "leaguePoints": 931
  }
];

function topThree(data) {

}

log(topThree(data)); // Должен вывести игроков BoostScooby, SaiyanBroadway, Mountaintrid

Шаг 2

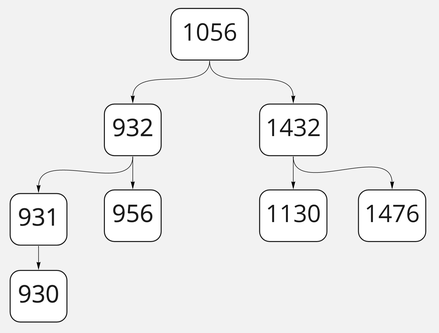
Мы уже знаем, в каком формате хранятся обычные деревья, нам нужно немного изменить их структуру и назвать детей каждой ноды по их положению — слева или справа. Построим следующее дерево из визуализации, представленной выше.

import {log} from "./logger";

const data = [
  {
    "login": "DreamLess",
    "leaguePoints": 956
  },
  {
    "login": "cavernous",
    "leaguePoints": 1056
  },
  {
    "login": "SaiyanBroadway",
    "leaguePoints": 1432
  },
  {
    "login": "Mountaintrid",
    "leaguePoints": 1130
  },
  {
    "login": "cathead",
    "leaguePoints": 930
  },
  {
    "login": "Goldenelox",
    "leaguePoints": 932
  },
  {
    "login": "BoostScooby",
    "leaguePoints": 1476
  },
  {
    "login": "JoshChase",
    "leaguePoints": 931
  }
];

// BST = Binary Search Tree
class BSTNode {
  constructor(value, left, right) {
    this.value = value;
    this.left = left;
    this.right = right;
  }
}

// просто для наглядности буду называть ноды по их пути в нашем новом дереве
const leftLeftLeft = new BSTNode(data[4], null, null);
const leftLeft = new BSTNode(data[7], leftLeftLeft, null);
const leftRight = new BSTNode(data[0], null, null);
const left = new BSTNode(data[5], leftLeft, leftRight);

const rightLeft = new BSTNode(data[3], null, null);
const rightRight = new BSTNode(data[6], null, null);
const right = new BSTNode(data[2], rightLeft, rightRight);

// "Корень" нашего дерева, будем обходить начиная с него
const root = new BSTNode(data[1], left, right);


function topThree(data) {

}

log(topThree(root)); // Должен вывести игроков BoostScooby, SaiyanBroadway, Mountaintrid

Шаг 3

Теперь наша задача довольно проста: нужно лишь найти самую правую часть дерева, у которой есть два потомка. Так как наше дерево самобалансируется, предположим, что у каждой правой ноды есть либо ноль, либо оба ребёнка.

import {log} from "./logger";

const data = [
  {
    "login": "DreamLess",
    "leaguePoints": 956
  },
  {
    "login": "cavernous",
    "leaguePoints": 1056
  },
  {
    "login": "SaiyanBroadway",
    "leaguePoints": 1432
  },
  {
    "login": "Mountaintrid",
    "leaguePoints": 1130
  },
  {
    "login": "cathead",
    "leaguePoints": 930
  },
  {
    "login": "Goldenelox",
    "leaguePoints": 932
  },
  {
    "login": "BoostScooby",
    "leaguePoints": 1476
  },
  {
    "login": "JoshChase",
    "leaguePoints": 931
  }
];

Шаг 4

Мы точно знаем, что у полученного нами корня лучшей тройки слева точно идёт самый маленький счет, справа — самый большой, а в самом корне — топ-2. Остается лишь вернуть их в нужной очерёдности.

import {log} from "./logger";

const data = [
  {
    "login": "DreamLess",
    "leaguePoints": 956
  },
  {
    "login": "cavernous",
    "leaguePoints": 1056
  },
  {
    "login": "SaiyanBroadway",
    "leaguePoints": 1432
  },
  {
    "login": "Mountaintrid",
    "leaguePoints": 1130
  },
  {
    "login": "cathead",
    "leaguePoints": 930
  },
  {
    "login": "Goldenelox",
    "leaguePoints": 932
  },
  {
    "login": "BoostScooby",
    "leaguePoints": 1476
  },
  {
    "login": "JoshChase",
    "leaguePoints": 931
  }
];

// BST = Binary Search Tree
class BSTNode {
  constructor(value, left, right) {
    this.value = value;
    this.left = left;
    this.right = right;
  }
}

// просто для наглядности буду называть ноды по их пути в нашем новом дереве
const leftLeftLeft = new BSTNode(data[4], null, null);
const leftLeft = new BSTNode(data[7], leftLeftLeft, null);
const leftRight = new BSTNode(data[0], null, null);
const left = new BSTNode(data[5], leftLeft, leftRight);

const rightLeft = new BSTNode(data[3], null, null);
const rightRight = new BSTNode(data[6], null, null);
const right = new BSTNode(data[2], rightLeft, rightRight);

// "Корень" нашего дерева, будем обходить начиная с него
const root = new BSTNode(data[1], left, right);


function topThree(root) {
  let bestThreeRoot = root;

  // пока снизу справа есть как минимум один уровень...
  while(bestThreeRoot.right && bestThreeRoot.right.right) {
    // ... обновляем указатель на лучшую тройку
    bestThreeRoot = bestThreeRoot.right;
  }

  return [bestThreeRoot.right.value, bestThreeRoot.value, bestThreeRoot.left.value];
}

log(topThree(root)); // Должен вывести игроков BoostScooby, SaiyanBroadway, Mountaintrid

File logger

const results = document.getElementById('results')

export function log(players) {
  for (const {login, leaguePoints} of players) {
    const result = document.createElement('li');

    result.innerHTML = `${login} со счетом ${leaguePoints}`

    results.appendChild(result);
  }
}